※ 本文を一部修正し、<補足説明>を本文の下に追加しました。('19.6.21)
※ 本文を一部修正しました。「遠心力」の記述を「慣性力」に改めました。('22.3.1)
1、潮汐力とは
形のある天体に働いて、天体の形を変形させることのできる力を潮汐力(tidal force)と呼んでいます。
潮汐(tide)とは海の潮の満ち引きの事です。例えば地球は主に月と太陽からの潮汐力を受けています。地球の海は流体なので変形しやすいのですが、固体部分も潮汐力により変形します。また、天体の形を保つ力よりも潮汐力が大きい場合、天体が破壊することもあります。例えば2013年に明るくなると期待されたアイソン彗星は近日点付近で暗くなってしまいましたが、その原因は太陽に接近した際に太陽による潮汐力と熱でバラバラに崩壊したからだと言われています。
2、潮汐力のしくみ
潮汐力とはどのような力なのでしょうか?地球上の2点に働く月からの引力を考えてみましょう。
力の法則によれば、月からの引力は月までの距離が近いほうが遠いほうよりも強くなりますので、その引力は下の図1のように描けます。月に一番近い点A、地球の中心B、一番遠い点C、では地球の半径の分だけ月からの距離が違うので、働く引力はこの順に弱くなっていきます。
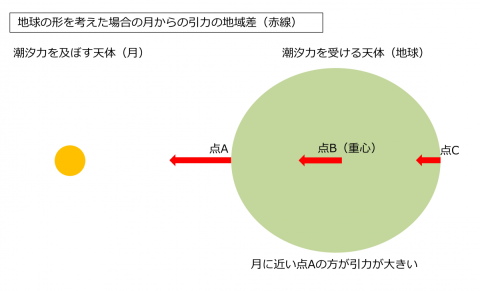
一方、地球を点とみなした場合、月からの引力は地球が<月―地球>重心のまわりを回るための駆動力になります。
話が少し飛びますが、まず「見かけの力」について説明します。例えばエレベータが下に動き出す時、体が持ち上げられるように感じることがあります。実際に私達に働いているのは下向きの力なのですが、エレベータと一緒に動く座標系にいる私達には逆に上向きの力が働いているように感じるのです。このような(座標系が違うことによる)見かけの力を物理の言葉では「慣性力」と言います。
話を戻します。地球にいる人から見ると、地球全体が<月―地球>重心のまわりを加速度運動しているために発生する「見かけの力」(慣性力)が、月とは反対の方向に働いているように感じます。
地球上のそれぞれの点は、<月―地球>重心のまわりを地球重心が回るのと同じように回るため(補足1)、その「見かけの力」の大きさはA,B,C地点いずれも、地球重心に働く月による引力と同じです(図2)。
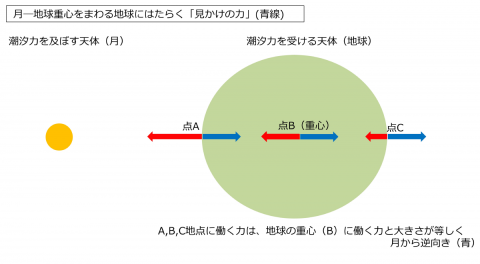
地球の形を考えた場合の月からの引力(赤線)と、<月―地球>重心をまわる地球にはたらく「見かけの力」(青線)との差が、形状を変形させる力としてそれらの地点に働きます(図3)。これが潮汐力です。
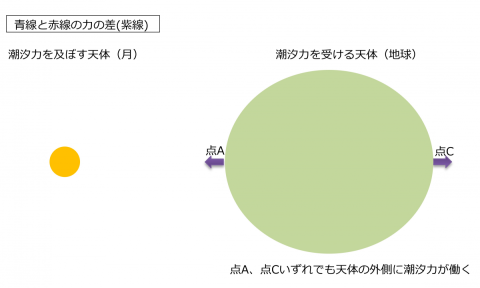
上では地球にいる人の立場で説明しましたが、月と地球を俯瞰できる固定した場所(座標系)で見た場合には、重心に働く力が<月―地球>重心のまわりを地球が回るための駆動力として作用し、その残りが形状を変形させる力になる、という言い方もできます。
地球には月だけでなく太陽からの潮汐力も働きます。その大きさは月の潮汐力の半分程度と無視できません。月―地球の距離変化と太陽―地球の距離変化は異なる周期を持っていますので、それぞれの周期に対応する潮汐力が地球に働き、異なる周期の潮の満ち引きを引き起こします。
3、潮汐変形
変形を引き起こすことができる力(潮汐力)と、結果として起こる海や固体部分の変形は区別する必要があります。潮汐力は天体の位置と形状が分かれば計算することができますが、変形は測定しないとわかりません。天体がとても硬い物質で出来ていれば(物理では「剛体」と呼びます)、天体は変形せずに元のままですし、変形が見られるとすれば剛体ではないと言えます。言い換えると、潮汐力による天体の変形の度合いを調べることにより天体の硬さがわかります。また、地球の海水の場合、陸と海の分布、海水が動く際の摩擦などの影響があり、実際の水の動きは複雑になります(参考リンク:測地学テキスト「海洋潮汐」)。海洋潮汐モデルを作る研究は多くなされており、日本発のものとしては国立天文台水沢のNAO.99bが有名です。
第二回以降では潮汐が主役となるいくつかの現象を説明したいと思います。
<補足説明>
補足1、図2の「見かけの力」がどの場所でも同じことの説明
月―地球系の場合、軌道運動は<月・地球>共通重心のまわりを約1か月で回る運動です。図Aにその様子をgifアニメーションで示します。赤い点が<月・地球>共通重心、濃い灰色が月、薄い灰色が地球、青矢印が地球と一緒に動く座標系で生じる見かけの力(慣性力)です。赤線は地球が自転をしていないことを表すための便宜的な線です。地球が共通重心のまわりを回りつつも、赤線そのものは回っていないことに注意しましょう。地球の質量は月よりもずっと大きいため、<月・地球>共通重心は地球の内部にあります。質量の中心に働く力が軌道運動に寄与します。

さて、慣性系(外力を受けない限り加速度が生じない座標系。本文では「月と地球を俯瞰できる固定した場所(座標系)」と記載したものです)で見ると、地球重心は、<月・地球>共通重心のまわりを円を描くように回っています。地球重心以外の点も、よく見ると、地球重心が回るのと同じ半径の円を描くように回っていることがわかります。地球にいる人の座標系(慣性系に対して加速度を持つので「非慣性系」)に乗り移って考えると、どの点でも同じ加速度運動をしていることから、同じ大きさの慣性力(青矢印)が働くことになります。
補足2、回転しない系での潮汐力
本文では、月―地球系の地球を例として潮汐力の説明をしました。我々は地球上におり、潮の満ち引きを通じて潮汐が実感できる最も身近な例だからです。月―地球系は<月・地球>共通重心のまわりを回る回転系ですが、例えばある惑星に向かってほぼ一直線に落下する天体があったとすると、この天体にも潮汐力は働きます(太陽系内に起源を持つ天体の場合は楕円運動になるため、この仮定は正確ではありませんが)。この場合も力の表記は全く同じで、落ちていく先の惑星に近い側により強い力が、遠い側により弱い力が働き、慣性系では落下に寄与する力の成分を分離した残りが潮汐力になります。