1.はじめに
満月の見かけの高さが低い、と最近(2023年の夏季)感じたことはありませんか?天文界隈のSNSではこのことが一時期話題になっていました。地球から見た月の軌道(白道)は黄道に近く、夏の星座であるいて座やさそり座が南に低く見えるのと同じで夏の夜の月は低く、冬の夜では高いのですが、今回の話題の効果が加わり、この後数年間でさらに低くなり、2025年頃の夏に一番低くなります。この話は最後に改めて書きます。
今回の読み物シリーズ「秤動」の付録回は月の自転と公転の法則であるカッシニの法則(Cassini’s laws)とカッシニ状態(Cassini state)の話です。これまで書いてきたように天体の一様な回転からのずれが秤動ですが、この「一様回転」とは何か?と聞かれた時の答えが「カッシニ状態」とも言えます。
2.月の自転を表すカッシニの法則
地球の月は球形ですから「おもて」「うら」はないはずですが、これまでの連載でも書いた通り、地球の潮汐力により月の自転と地球を回る公転の時間が同じになって、月の一面がいつも地球に向いています。そのため地球に向いた面を慣習的に「おもて」と呼んでいます。自転と公転の時間が同じになる現象は「自転と公転の共鳴」とか、月の回転が地球にロック(固定)されるので「潮汐ロック」などと呼ばれたりします。
17世紀にはすでにジョバンニ・ドメニコ・カッシニ(イタリア生まれの天文学者で、フランスに移住してジャン=ドミニク・カッシニ)により、月の自転の法則がまとめられていました。これが「カッシニの法則」です。法則は3つあります。表現方法は複数あるのですが、国立天文台・暦計算室の暦wiki[1]からそれぞれ冒頭部分だけを引用すると以下の通りです。
---
1.月の自転速度は公転の平均運動に等しい
2.月の赤道面は黄道面に対して一定の角度(約1.5°)を保つ
3.月の自転軸、月の公転面の法線、黄道面の法線は常に同一平面内にある
---
1は自転と公転の周期が同じであること、つまり先に書いた月のおもて面が地球に向くことです。2と3は表現が難しいので、順番に説明してみます。
3.カッシニの法則2
「2.月の赤道面は黄道面に対して一定の角度(約1.5°)を保つ」
【赤道面とは?】
月の赤道は月面での緯度がゼロの線で、定義は地球の赤道と同じです。「赤道面」は天文学の用語で、赤道の線を天球(宇宙)に投影した時の円のことです。自転軸の極を天球に投影した点が「天の北極(南極)」で、それに垂直な面なので、天体の自転軸に垂直な方向を表しています。この法則では「月の」赤道面と書いてあるので、地球ではなくて月の回転軸に垂直な面のことを言っています。
【黄道面とは?】
一方、黄道(こうどう)面は地球から見た時の太陽の軌道を天球(宇宙)に投影した面のことです。黄道十二星座といえば、黄道面に沿った星座で(おひつじ座、おうし座、…みずがめ座、うお座)、星占いにも使われている事はご存じの方も多いと思います。
地球を中心とする天球ではなくて実際の太陽が中心の宇宙空間で考えると、月は地球の周りを回りながら、同時に地球と月は一緒に太陽の周りも回っています。地球(と月)が太陽の周りをまわる軌道は地球から見ると黄道です。頭がこんがらがりますが、法則2は「地球(と月)が太陽の周りをまわる軌道に対して、月の自転軸は1.5度を保っている」、ということになります([2]に補足)。地球の周りをまわる軌道に対してではなく、太陽の周りをまわる軌道に対して角度が同じになる、というのが何か不思議な気がしますね。。。
4.カッシニの法則3
「3.月の自転軸、月の公転面の法線、黄道面の法線は常に同一平面内にある」
法則3は月の自転と2つの軌道面の関係を表すもので、これが「カッシニ状態」を表します。法線(ほうせん)とは軌道面に垂直な方向のことです。この表現では面と面を比べるかわりに、それらの垂直な線である法線同士を比べています。
まず図をご覧ください。図右上の位置に描かれた月の中心から延びる3本の線「月軌道面法線」、「黄道面法線」、「自転軸」が一つの面に収まる、というのが法則3です。線が三本あるとカメラの三脚のように立体的になりそうですが、そうならないのです。「月の公転面(=軌道面)の法線」は月が地球の周りをまわる軌道に垂直な方向、「黄道面の法線」は地球(と月)が太陽の周りをまわる軌道に垂直な方向です。
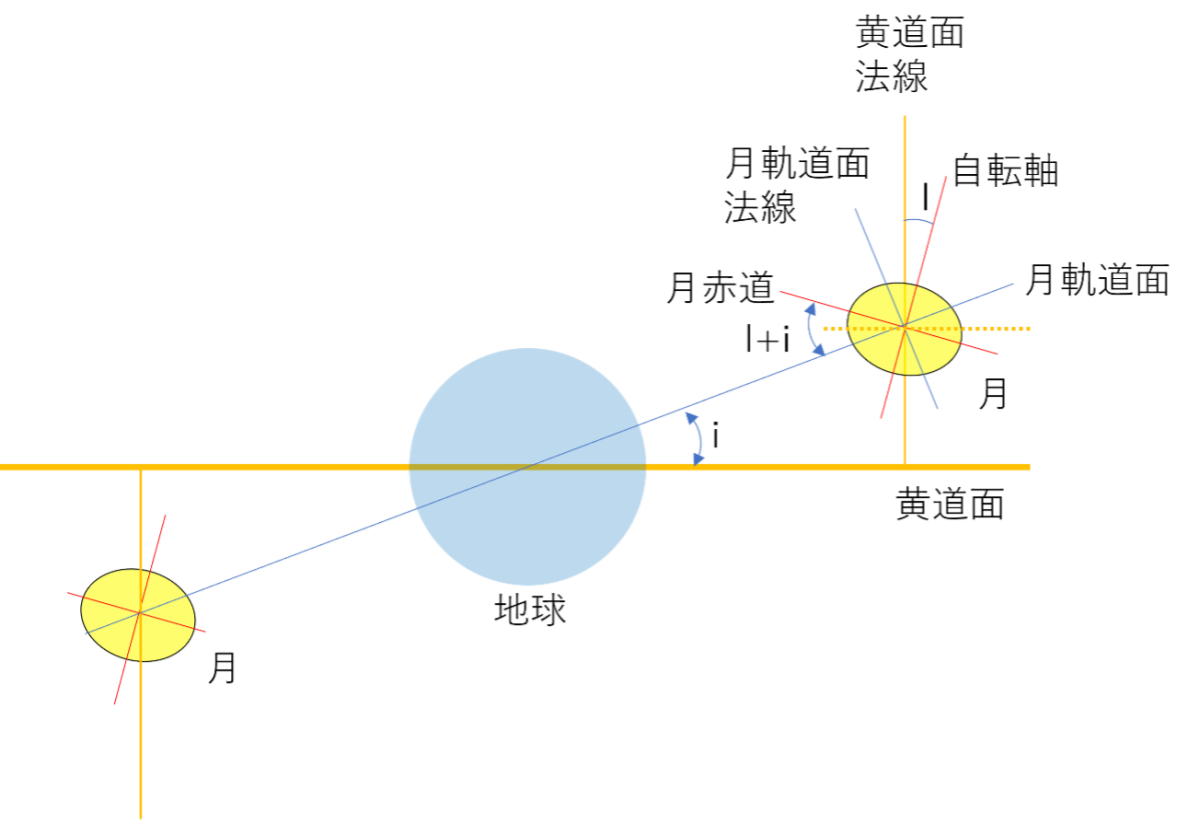
図:月の軌道と自転を表す図([3]を参考に作成)。小文字のi(=5.1度)は軌道傾斜角(inclination)、I+iは赤道傾斜角(軌道面に対する赤道の傾き, obliquity, 6.6度)を表します。大文字のI(=1.5度)は黄道面法線方向に対する自転軸の傾きです。
この3本が同じ平面にある、ということは何を表すのでしょうか?
回転するコマの軸が首振り運動をするように、月の自転軸も同じような歳差運動(みそすり運動)をします([4] に補足)。その際、法則2から月の自転軸の方向は黄道面の法線方向から1.5度を保ちます。黄道面は(ほぼ)変わらないので黄道面法線は固定で、月軌道面法線、黄道面法線と月自転軸が同一平面になるということは、自転軸と同じように、月の軌道面も黄道面に対して同じ周期の歳差運動をする、ということになります。カッシニ状態は月だけでなく、自転周期と公転周期が2:3の共鳴状態にある水星でも成り立っていることが知られています。
ある面に対して軌道面が下から上に横切る点を昇交点、上から下に横切る点を降交点と呼びますが、法則3を言い換えると「月の軌道面の昇交点と月赤道の降交点が一致する」、となります。図の右上の月に描いた黄道面(黄色の点線)を月軌道面、月赤道面が同じ位置でそれぞれ上、下に横切っている様子が分かるかと思います。
さて、本シリーズのテーマは「秤動」でした。月には物理秤動がありますから、実際にはこの3本の線が完全に同一平面に収まるわけではありません。逆にいうと、カッシニ状態からのずれが月の物理秤動を表している、とも言えます( [5] に補足)。
5.おわりに ~月の見かけの高さの続き~
冒頭の「最近、月の見かけの高さが低い」という話の続きです。法則3の説明で月の軌道面が歳差運動することを書きました。これを地球にいる私達から見ると、18.6年かけて月の見かけの高度が平均の位置からプラス5.1度、マイナス5.1度、合計で10.2度変化する、ということになります。暦計算室の該当ページ[6]の「満月の南中高度」の図にあるように、確かに夏至に近い満月の高度の差が10度くらいであることがわかります。月の見かけの直径は0.5度、腕を伸ばしたげんこつの幅を空にかざすとそれがだいたい10度ですから、長年月に親しんでいる方には気が付くくらいの大きさと言えるでしょう。月の自転軸の運動は幾何秤動に埋もれて気が付かないですが、月自転の法則がこのような形で目に見えるのは面白いのではないかと思います。
参考・サイト
[1] 国立天文台暦計算室「カッシニ(Cassini)の法則」ページ
https://eco.mtk.nao.ac.jp/koyomi/wiki/A5ABA5C3A5B7A5CBA4CECBA1C2A7.html
[2] 少し話題がずれますが、地球の赤道が公転軌道に対してなす角度(赤道傾斜角)は23.4度なので、夏と冬で太陽の高さが大きく違い、また白夜・極夜となる地域は緯度66.6度以北(以南)となります。一方で、月の自転軸の黄道面に対する傾きは1.5度しかありませんので太陽高度の季節変化は地球に比べて小さく、また月の極域で白夜・極夜になる地域は地形を考慮しない場合に緯度88.5度以上のごく狭い範囲になります。
[3] Eckhardt (1981) The Moon and the Planets 25, 3-49.
[4] 地球の自転軸も約2万6千年の周期の歳差運動をするので、今から約1万2千年後にはこと座の一等星ベガが天の北極に近づいて「北極星」となることをご存じの方もおられると思います。月自転の歳差運動の周期はもっと短く、18.6年です。
[5] Williams et al. (2001) Journal of Geophysical Research106, 27,933-27,968によると、カッシニ状態からのずれの観測値は月の自転軸で測ると0.263秒角、月軌道の昇交点位置のずれで測ると-9.8秒角となります。
[6] 国立天文台暦計算室「最北と最南」ページ
https://eco.mtk.nao.ac.jp/koyomi/wiki/B7EEA4CEB8F8C5BEB1BFC6B02FBAC7CBCCA4C8BAC7C6EE.html
(文責:野田 寛大)