前回は、探査機の軌道を決めることがなぜ大切なのか、そしてそのためにどんなデータが必要かを説明しました。今回は、集めたデータを使って実際に探査機の軌道をどうやって決めるのかをお話しします。
(1)2体問題の場合
まずは、もっとも簡単な「2体問題」を考えましょう。これは、探査機と天体の2つだけを考え、探査機が天体の周りを周回している場合です。この場合、探査機は天体の引力(重力)だけを受けて動きます。このシンプルな状況では、探査機の軌道は比較的簡単に計算できます。
解析的な方法
探査機が軌道上のどこにいるかを示すために、次の6つの軌道要素を使います。
- 軌道長半径 (a): 楕円の長い方の半分の長さです。
- 離心率 (e): 軌道の形を示します。どれくらい楕円がつぶれているかを表します。
- 軌道傾斜角 (i): 軌道の傾きを示します。これは、軌道が天体の赤道面に対してどれくらい傾いているかを表します。
- 昇交点赤経 (Ω): 軌道が赤道を横切る地点の角度です。これは、軌道がどの方向にあるかを示します。
- 近地点引数 (ω): 軌道上で天体に一番近い地点までの角度です。これは、軌道のどの部分が天体に一番近いかを示します。
- 真近点離角 (ν): 天体に一番近い地点から探査機の今の位置までの角度です。
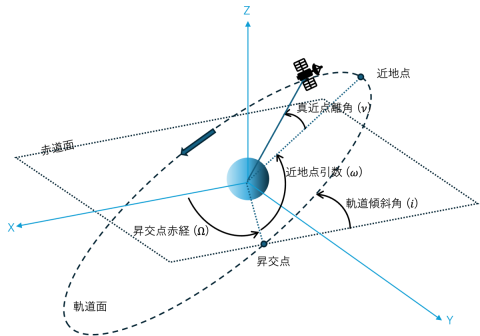
図1
軌道長半径と離心率は、平面上の軌道の形を決め、軌道傾斜角、昇交点赤経、近地点引数は軌道を3次元空間に配置します。真近点離角は軌道上の探査機の場所を現す要素です(図1)。
2体問題では、時間が経つと変わるのは6つの要素のうちの「真近点離角」だけです。その他の要素は、時間とともに変わりません。最初に探査機がどこにいたかがわかっていれば、その後の探査機の位置は、経過時間から比較的簡単に計算できます。これによって、探査機がある時刻にどこにいるかがわかります。
数値積分による方法
探査機の軌道を計算するもう一つの方法は「数値積分」です。これは、探査機の位置と速度を少しずつ計算していく方法です。この場合、探査機が軌道上のどこにいるかを表すのに、軌道要素の代わりに位置と速度を使う方が簡単に計算できます。軌道要素を使った表現と位置、速度を使った表現は相互に変換でき、状況に応じて使い分けられます。
ある時刻で探査機がどこにいて(位置)、どれくらいの速さで動いているか(速度)がわかっているとします。
まず、探査機にどんな力が働いているかを考え、その力によって探査機の速さがどう変わるか(加速度)を計算します。2体問題の場合は、中心の天体からの重力だけを考えればよく、加速度は、位置から簡単に計算できます。これらの位置、速度、加速度をもとにして、少し後の時間の探査機の位置と速度を計算します。
次に、新しく計算された位置、速度での、加速度を計算します。そしてこれらをもとにして、さらに少し後の時間の探査機の位置と速度を計算します。
このようにして少しずつ時間を進めながら、探査機の位置と速度を繰り返し計算していきます。この方法を使うと、将来のある時点で探査機がどこにいるかを知ることができ、解析的な方法と同じ結果を得ることができます(図2)。
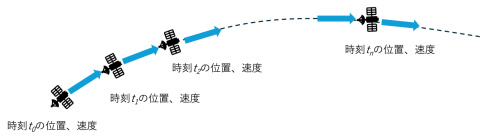
図2
(2) 現実の探査機の軌道
実際の探査機の軌道計算はもっと複雑です。なぜなら、第2回で述べたように、探査機は天体の重力以外にも様々な力を受けて運動しているからです。これらの影響により、真近点離角以外の軌道要素も時間により変化し、解析的な方法で軌道を計算することができなくなります。
そこで、数値積分による方法を使います。この場合、積分に必要な加速度は、中心の天体からの重力だけでなく、探査機が受けるすべての力を考え、それぞれの力による加速度を計算し、合計して使う必要があります。数値積分による方法なら、このように複雑な影響も考慮して軌道を計算することができます。計算は煩雑ですが、現実の状況に適した方法です。
(3)軌道決定
数値積分を使えば、現実の探査機の軌道も計算することができることがわかりましたが、こうして計算された軌道は本当に正しいのでしょうか。それ確認するためには、観測データを使います。
たとえば、ある時刻に地上の観測局から探査機までの距離を観測したとします。地上の観測局の座標が正しくわかっているとすると、これと同じ距離は、軌道計算によって得られた同じ時刻の探査機の位置を使えば計算できます。もしも計算された軌道が正しいものであるとするならば、観測された距離と、計算された距離は同じ値になり、差はゼロとなるはずです。もし、差がゼロとならなければ、計算に使った探査機の位置が間違っているということです(図3)。ということは、軌道計算の出発点の位置、速度が間違っているか、加速度の計算が間違っているということです。こうした評価は、距離だけでなく、他の観測データ(距離の変化、角度など、第2回を参照)を使っても同様に行うことができます。
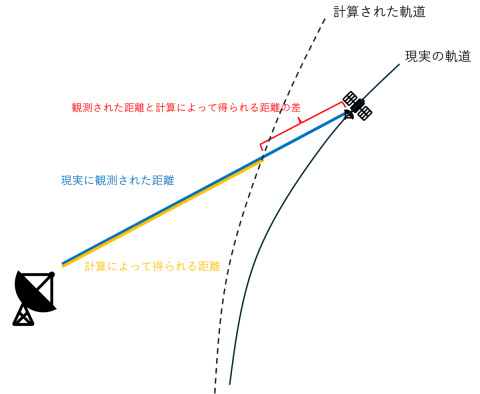
図3
計算された軌道の間違いを修正して、より現実に近い軌道を求める作業のことを軌道決定(あるいは軌道推定)といいます。多数の時刻で観測データと計算された値との差ができるだけ小さくなるように出発点の位置、速度と、各時刻の加速度計算に使うモデルを調整します。これらを使って改めて数値積分で軌道を計算することで、観測データとよく合うような、現実に近い軌道を得ることができます。
また、調整された加速度モデルの中には、天体の重力や回転状態などを示す要素も含まれています。現実に近い軌道を得るために調整されたこれらの要素は、より正確な値に近づいているはずです。こうして、軌道決定を通じて、天体の内部構造や運動状態をより正しく推定する手がかりを得ることが可能となります。
(文責:山本 圭香)